Árboles de Expansión

Created in January 08, 2023 by Alan Yahir Juárez Rubio , last updated in June 06, 2024

2023   ·   arbol   expansion-minimo   expansion-maximo   prim   kruskal   flujo-maximo   ·   matematicas   matematicas-discretas   arboles

Arbol de Expansión Mínimo

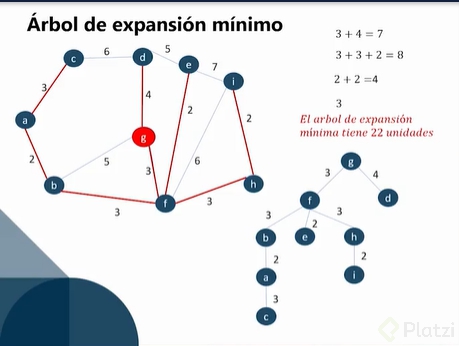
Un árbol de expansión mínimo es aquel árbol que partiendo de una raíz pueda conectar todos los vértices buscando los caminos de menor costo. Para sacar el costo mínimo del árbol solo basta con ir sumando el valor que tiene cada conexión nivel por nivel, luego sumar todos los niveles.

Arboles de Expansión Mínimo
Fig. 1: Árbol de expansión mínimo

Algoritmo de Prim

A continuación los pasos del algoritmo de Prim:

  1. Escoger un nodo cualquiera.
  2. Escoger el nodo asociado al nodo elegido previamente que tengan menor valor, menor coste.
  3. En cada iteración selecciona la arista de menor peso relacionado con los nodos conectados.
  4. Finaliza cuando todos los nodos están conectados con \(n-1\) aristas, donde \(n\) es el número de nodos.
  5. Para conseguir el coste total suma todas los valores de las aristas seleccionadas.
Algoritmo de Prim
Fig. 2. Algorimto de Prim

Coste total: 27

Algoritmo de Kruskal

El algoritmo de Kruskal al igual que el algoritmo de Prim sirve para buscar el árbol de expansión mínimo, la diferencia es que el algoritmo de Kruskal inicia seleccionando la arista de menor valor y después en cada iteración se agrega la arista de menor valor del conjunto disponible.

A continuación los pasos del algoritmo de Kruskal:

  1. Selecciona la arista menor.
  2. En cada iteración agruegue la arista de menor longitud del conjunto de arcos disponibles.
  3. El algoritmo finaliza cuando todos los vertices están conectados con \(n-1\) arcos.
Algoritmo de Kruskal
Fig. 3. Algoritmo de Kruskal
NOTA

Aplica para el agoritmo de prim y el de kruskal:

  • Cabe mencionar que cuando estemos haciendo este proceso no se formen ciclos cerrados o rutas cerradas porque sino se estarían repitiendo caminos por los cuales no se deberian pasar.
  • Esta conexión no es de orden secuencial, por lo que puedes hacer un camino y si se presenta algun ciclo o ruta cerrada, puedes regresarte a cualquiera de los demás nodos que ya han sido conectados y seguir conectando aquellos que no están conectados.

Árbol de Expansión Máximo

A diferencia del árbol de expansión mínimo, el cual busca conectar todos los nodos entre sí con la menor cantidad de recursos, este lo que busca es conseguir descifrar la cantidad máxima de recursos que se pueden mandar desde un punto inicial hasta un final a partir de los caminos que se disponen y sus respectivos flujos.

Algoritmo de Flujo Máximo

El algoritmo de flujo máximo consiste en los siguientes pasos:

  1. Direccionar los flujos e iniciar en ceros.
  2. Obtener trayectorias buscando el mayor flujo.
  3. Escoger el menor flujo de la trayectoria, esto es la arista de menor valor dentro de tu camino que seleccionaste.
  4. Actualizar el gráfico con las capacidades mínimas, ósea, restando el valor de la arista del anterior paso a cada una de las aristas del camino.
  5. Buscar nueva trayectoria o camina en aumento y repetir hasta que no existan más.
Algoritmo de Flujo Máximo
Fig. 4. Algoritmo de Flujo Máximo

Referencias



    Enjoy Reading This Article?

    Here are some more articles you might like to read next:

  • Introducción a los Comandos
  • Interfaces de Usuario en los Sistemas Operativos
  • Introducción a Linux
  • Introducción a los Sistemas Operativos
  • Vim CheatSet
  • Sistemas Numéricos