Formulario Precálculo
- Conjunto de Números Reales
- Leyes de los Exponentes
- Leyes de los Radicales
- Número Imaginario
- Operaciones con Polinomios
- Binomio de Newton
- Késimo Término
- Factorización
- Operaciones con Números Complejos en Forma Algebraica
- Intérvalos y Desigualdades
- Ecuaciones Cuadráticas (de Segundo Grado)
- Fracciones Parciales
- Referencias
- Recursos Recomendados
En este formulario: \(A, B, C, D, a, b, c, d, p, q, s \in \Bbb R\) y son constantes; \(n, m \in \Bbb{Z}\) y \(r \in \Bbb{Z}^+\)
Conjunto de Números Reales
Propiedades de los Números
| Suma | Multiplicación | |
|---|---|---|
| Ley conmutativa | \(a+b = b+a\) | \(a \cdot b = b \cdot a\) |
| Ley asociativa | \((a+b)+c = a+(b+c)\) | \((a \cdot b) \cdot c = a \cdot(b \cdot c)\) |
| Elemento Neutro | \(a+(0) = a\) | \(a \cdot (1) = a\) |
| Elemento inverso (recíproco) | $ a+(-a) = 0 $$ | \(a \cdot \left(\cfrac {1}{a} \right) = 1\) |
| Ley distributiva de la multiplicación con respecto de la suma | \((a+b \cdot c = a \cdot c+b \cdot c\) | \(\leftarrow\) |
Fracciones
\[\begin{align} \cfrac {a}{b} + \cfrac {c}{b} &= \cfrac {a + c}{b} \tag{Suma con mismo denominador} \\ \cfrac {a}{b} + \cfrac {c}{d} &= \cfrac {ad + bc}{cd} \tag{Suma con distinto denominador} \\ a + \cfrac {c}{b} &= \cfrac {ab + c}{b} \tag{Suma con entero y una fracción} \\ \cfrac {a}{b} \cdot \cfrac {c}{d} &= \cfrac {ac}{bd} \tag{Multiplicación de fracciones} \\ \cfrac {a}{b} \div \cfrac {c}{d} &= \cfrac {ad}{bc} \tag{Division de fracciones (cruzada)} \\ \cfrac {a}{b} \cdot \cfrac {c}{c} &= \cfrac {a \cdot c}{b \cdot c} = \cfrac {a}{b} \tag{Multiplicación por unidad} \end{align}\]Desigualdades
\[\begin{align} \text{ Si } a-b = c \to a > b, \;\; \text{ donde } c > 0 \tag{Mayor que} \\ \text{ Si } a-b = c \to a < b, \;\; \text{ donde } c < 0 \tag{Menor que} \\ \end{align}\]Valor Absoluto
\[|a| = \begin{bmatrix} a \geq 0 \to |a| &= a \\ a < 0 \to |a| &= -a \end{bmatrix}\]Distancia entre Dos Puntos
\[\begin{gather*} d(A,B) = |b-a| \\ d(B,A) = |a-b| \end{gather*}\]Leyes de los Exponentes
| Nombre | Ley |
|---|---|
| Ley de separación | \((\cfrac {a}{b})^n = \cfrac {a^n}{b^n}\) |
| Ley de separación | \((ab)^n = a^n b^n\) |
| Multiplicación de bases iguales | \(a^n a^m = a^{n+m}\) |
| Potencia de una base con potencia | \((a^n)^m = a^{nm}\) |
| Potencia cero | \(a^0 = 1\) |
| Potencia negativa | \(a^{-n} = \cfrac {1}{a^n}\) |
| División de bases iguales | \(\cfrac {a^n}{a^m} = a^{n-m} \ (si \ n > m)\) |
| División de bases iguales | \(\cfrac {a^n}{a^m} = \cfrac {1}{a^{m-n}}\) |
| De reescritura | \(a^{m/n} = \sqrt [n]{a^m}\) |
Leyes de los Radicales
| Nombre | Ley |
|---|---|
| De separación | \(\sqrt [n]{ab} = \sqrt [n]{a} \sqrt [n]{b}\) |
| De la raíz m_ésima de la raíz n_ésima | \(\sqrt [m] {\sqrt[n]{a}} = \sqrt [nm] {a}\) |
| De cancelación | \((\sqrt [n]{a})^n = a\) |
| De cancelación | \(\sqrt [n]{a^n} = (a^n)^{1/n} = a\), si \(n\) es impar |
| De cancelación | \(\sqrt [n]{a^n} = (a^n)^{1/n} = \mid a \mid\), si \(n\) es par |
| De reescritura | \(\sqrt [n]{a^m} = a^{m/n}\) |
ADVERTENCIA
\[\sqrt [n]{a^n \pm b^n} \neq a \pm b\] \[\sqrt [n]{a \pm b} \neq a \pm b\]
Número Imaginario
Número imaginario: \(i = \sqrt{-1}\)
\[\begin{array}{l} i^0 &= 1 \\ i^1 &= i \\ i^2 &= -1 \\ i^3 &= i^2i &= (-1)i &= -i \\ i^4 &= i^2 i^2 &= (-1)(-1) &= 1 \end{array}\]Número complejo: \(z = a+bi \mid a \in \Bbb R \text{ y } bi \in \Bbb I \to z \in \Bbb C\)
Operaciones con Polinomios
\[\begin{align} ab^n \pm b^n &= b^n(a \pm 1) \tag{Suma y resta (términos semejantes)} \\ a(b+c) &= ab + ac \tag{Multiplicación} \end{align}\]Productos Notables
| Nombre | Expresión | Equivalencia |
|---|---|---|
| Diferencia de cuadrados | \(a^2 - b^2\) | \((a-b)(a+b)\) |
| Suma de cubos | \(a^3 + b^3\) | \((a+b)(a^2 - ab + b^2)\) |
| Diferencia de cubos | \(a^3 - b^3\) | \((a+b)(a^2 + ab + b^2)\) |
| Binomio al cuadrado | \((a+b)^2\) | \(a^2 + 2ab + b^2\) |
| Binomio al cuadrado | \((a-b)^2\) | \(a^2 - 2ab + a^2\) |
| Binomio al cubo | \((a+b)^3\) | \(a^3 + 3a^2b + 3ab^2 + b^3\) |
| Binomio a la cuarta | \((a+b)^4\) | \(a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4\) |
Binomio de Newton
\[(a+b)^n = a^n + \cfrac {n}{1!}a^{n-1}b + \cfrac {n(n-1)}{2!}a^{n-2}b^2 + \cfrac {n(n-1)(n-2)}{3!}a^{n-3}b^3 + \cdots + b^n\]Késimo Término
\[K_{\text{ésimo}} \text{ término } = \cfrac {n!} {(n-r+1)!(r-1)!} \cdot a^{n-r+1} \cdot b^{r-1}\]NOTA
donde:
- \(n =\) potencias.
- \(r\) = número del término a buscar.
- \(n,r \in \Bbb{Z}^+\).
Factorización
Por fórmula: Consultar las fórmulas de productos notables.
Por término común: \(x^2 + ax = x(x+a)\)
Por agrupación:
\[\begin{gather*} ax + bx + ay + by \\ (ax + bx) + (ay + by) \\ x(a + b) + y(a + b) \\ (a + b)(x + y) \\ \end{gather*}\]Operaciones con Números Complejos en Forma Algebraica
\[\begin{array}{c|c|c} \ \text{Suma y resta} & \text{División} & \text{Multiplicación} \\ \eqalign { z_1 + z_2 &= (a+bi)+(c+di) \\ &= (a+c)(b+d)i \\ \\ z_1 + z_2 &= (a+bi) - (c+di) \\ &= (a-c) + (b-d)i } & \eqalign { \cfrac {z_1}{z_2} &= \cfrac {z_1}{z_2} \cdot \cfrac {z_2}{x_2} \\ &= \cfrac {a + bi}{c + di} \cdot \cfrac {c-di}{c-di} \\ &= \cfrac {ac + (bc-ad)i-bdi^2}{c^2 d^2 i^2} } & \eqalign{ z_1 \cdot z_2 &= (a + bi)(c + di) \\ &= ac + bci + adi + bdi^2 \\ &= ac + (bc + ad) + bdi^2 \\ } \end{array}\]Intérvalos y Desigualdades
Intérvalos
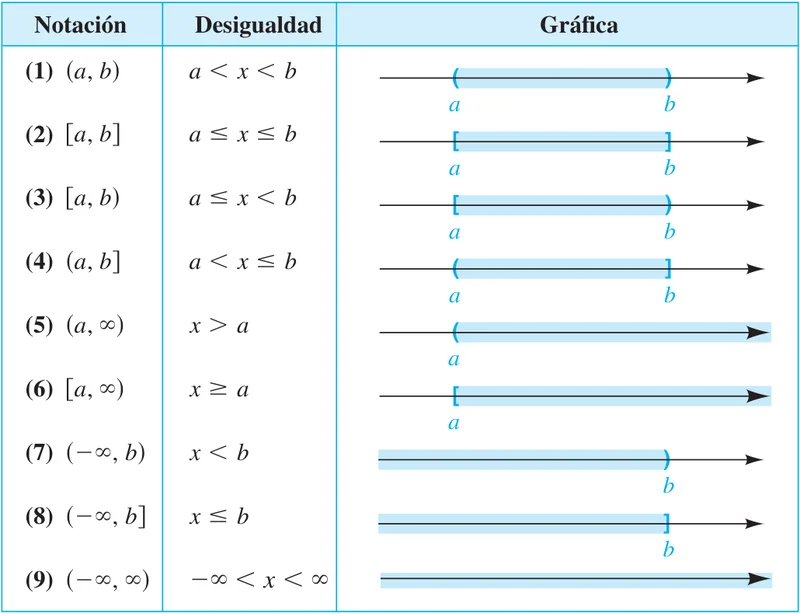
Desigualdades
- Si \(a > b\) y \(b > c\), entonces \(a > c\)
- Si \(a > b\), entonces \(a+c > b+c\)
- Si \(a > b\) y \(c > 0\), entonces \(ac > bc\)
- Si \(a > b\) y \(c < 0\), entonces \(ac < bc\)
NOTA
Al multiplicar o dividir ambos lados de una desigualdad por un número real negativo, el signo de la desigualdad se invierte.
Desigualdad con Valor Absoluto
| Caso | Modelo | Solución |
|---|---|---|
| 1 | \(\mid a \mid < b\) | \(-b < a < b\) |
| 2 | \(\mid a \mid \leq b\) | \(-b \leq a \leq b\) |
| 3 | \(\mid a \mid > b\) | \(a < -b \cup a > b\) |
| 4 | \(\mid a \mid \geq b\) | \(a \leq -b \cup a \geq b\) |
Ecuaciones Cuadráticas (de Segundo Grado)
Completar el Cuadrado
| Expresión original | Término a sumar | Expresión Transformada | Equivalencia |
|---|---|---|---|
| \(x^2 + kx\) | \(\left(\cfrac {k}{2} \right)^2\) | \(x^2 + kx + \left(\cfrac {k}{2} \right)^2\) | \(\left(x + \cfrac {k}{2} \right)^2\) |
| \(x^2 - kx\) | \(\left(\cfrac {k}{2} \right)^2\) | \(x^2 - kx + \left(\cfrac {k}{2} \right)^2\) | \(\left(x - \cfrac {k}{2} \right)^2\) |
Fórmula General
\[\begin{gather*} x = \cfrac {-b \pm \sqrt {b^2 - 4ac}} {2a} \tag{Para $ ax^2 + bx + c = 0, a \neq 0 $ } \end{gather*}\]Discriminante
\[D = b^2 - 4ac\]- \(D \mid D > 0 \Rightarrow\) Dos soluciones reales
- \(D \mid D < 0 \Rightarrow\) Dos soluciones complejas
- \(D \mid D = 0 \Rightarrow\) Solución repetida, una única solución
Método de Po-Shen Loh
\[ax^2 + bx + c = d\]Para factorizar esto podemos buscar dos números que multiplicados den \(c\) y sumados den \(b\). Se puede hacer por prueba y error o aplicando el método de Po-shen Lo:
- Dividimos toda la expresión entre \(a\)
- Buscamos dos números que sumados den \(\cfrac {b}{a}\), lo más sencillo es hacer cada uno de estos dos números dos números valgan la mitad de \(\cfrac {b}{a}\)
- Le sumamos a \(p\) una cantidad, pero a \(q\) se le resta esa misma cantidad para mantener el equilibrio
- Buscamos los dos números que multiplicados den \(\cfrac {a}{c}\)
- Despejamos respecto a \(s\)
- Tomamos el valor de \(s\), ya sea el positivo o el negativo.
- Ahora solo sustituimos \(s\)
Entonces tenemos que
\[\begin{gather*} x^2 + \cfrac {bx}{a} + \cfrac {c}{a} = \cfrac {d}{a} \\ \left(x + \cfrac {b + \sqrt{b^2 - 4ac}} {2a} \right) \left(x + \cfrac {b - \sqrt{b^2 - 4ac}} {2a} \right) = \cfrac {d}{a} \\ \end{gather*}\]Valor Absoluto
\[\begin{gather*} |x| = y \\ x = \pm y \end{gather*}\]NOTA
La raíz cuadrada de una variable elevada al cuadrado te da su valor absoluto, a menos que se sepa de antemano que dicha variable es positiva o negativa.
\[\begin{gather*} \sqrt{x^2} = |x| \\ \sqrt{x^2} = x, x > 0 \\ \sqrt{x^2} = - x, x < 0 \end{gather*}\]
Por Agrupación
\[\begin{gather*} x^2 + ax + bx + ba = 0 \\ x(x+a) + b(x+a) = 0 \\ (x+a)(x+b) = 0 \end{gather*}\]Teorema del Cero
Un producto que da 0 solo puede ser posible si por lo menos uno de los factores es 0
Una variable:
\[\begin{gather*} (x+a)(x+b) = 0 \\ \\ \ \begin{array}{l|l} \text{Sol. 1} & \text{Sol. 2} \\ \ x+a = 0 & x+b = 0 \\ x_1 = -a & x_2 = -b \end{array} \end{gather*}\]Dos variables
\[\begin{gather*} (x+a)(y+b) = 0 \\ \\ \ \begin{array}{l|l} x+a = 0 & y+b = 0 \\ x = -a & y = -b \end{array} \end{gather*}\]En este caso puede haber 3 posibles soluciones:
\[\begin{gather*} x = -a, y = c, \tag{donde $ c $ puede tener cualquier valor} \\ y = -b, x = d, \tag{donde $ d $ puede tener cualquier valor} \\ x = -a, y = -b \\ \end{gather*}\]RECOMENDACIÓN
Recuerda siempre hacer comprobación de todas las posibles soluciones para determinar cuál es la solución que satisface la ecuación.
Por Sustitución
\[ax^4 + bx^2 + c = 0\]- Aplicar sustitución para simplicar la ecuación original
- Resolver la ecuación
- Sustituir por los valores originales
- Comprobación
Fracciones Parciales
Siendo el grado de \(f(x)\) menor que el de \(g(x)\), entonces tenemos que
\[\cfrac {f(x)}{g(x)} = F_1 + F_2 + \cdots + F_r\]tal que \(F_k\) tiene una de las formas:
\[\cfrac {A}{(ax + b)^n} \\ \text{ o } \\ \cfrac {A_x + B}{(ax^2 + bx + c)^n}\]Factores lineales distintos:
\[\cfrac {f(x)}{(ax + b)(cx + d) \cdots} = \cfrac {A}{ax + b} + \cfrac {B}{cx + d} + \dots \tag{1}\]Factores lineales repetidos:
\[\cfrac {f(x)}{(ax + b)^n} = \cfrac {A}{ax + b} + \cfrac {B}{(ax + b)^2} + \cdots \tag{2}\]Factores cuadráticos distintos:
\[\cfrac {f(x)} {(ax^2 + bx + c)(dx^2 + cx + f)} = \cfrac {Ax + B} {ax^2 + bx + c} + \cfrac {Cx + D} {dx^2 + ex + f} + \cdots \tag{3}\]Factores cuadráticos repetidos:
\[\cfrac {f(x)} {(ax^2 + bx + c)^n} = \cfrac {Ax + B} {ax^2 + bx + c} + \cfrac {Cx + D} {(ax^2 + bx + c)^2} + \cdots \tag{4}\]Procedimiento General
- Asegurarse que el grado del numerador \(f(x)\) sea menor que el del denominador; de ser el caso contrario, aplicar la división larga.
- Factorizar el denominador en factorles lineales \(px + q\) o factores cuadráticos irreducibles.
- Multiplicar los númeradores de cada \(F_k\) por el mínimo común múltiplo, es decir, por cada uno de los factores, para poder convertir la expresión en líneal.
- Igualar la expresión encontrada por el numerador \(f(x)\).
- Convertir la expresión en la forma:
- Considerando que \(f(x) = b_1x + b_2 x^2 + \cdots\), entonces podemos igualar los coeficientes de las potencias semejantes.de esta manera obtenemos un sistema de ecuaciones.
- Sustituir en las fracciones parciales los valores de \(A, B, \cdots\).
Factores Lineales no Repetidos
En caso de que todos los factores del denominador sean lineales no repetidos \((1)\), entonces podemos aplicar un método alternativo a partir del paso 4.
- Sustituir los valores de \(x\) que hagan que cada uno de los factores lineales se conviertan en 0.
- Resolver cada caso haciendo las sustituciones necesarias.
- Sustituir en las fracciones parciales los valores de \(A, B, \dots\)
Referencias
-
W., E. & A., J. (2009). Álgebra y trigonometría con geometría análitica (12a ed.). En S. R. Cervantes (Ed.), Editorial CENGAGE Learning.
-
Standen Math. (mayo 23, 2022). La mejor manera de resolver una ecuación cuadrática. Recuperado el 22 de abril de 2023 de https://www.youtube.com/watch?v=GFO6FCbSCyo
Recursos Recomendados
Enjoy Reading This Article?
Here are some more articles you might like to read next: